粒子群智能算法(Particle Swarm Optimization,PSO)是一种优化算法,它模拟了鸟群或鱼群等生物群体的行为,通过不断地迭代来逐步优化问题的解。该算法由Kennedy和Eberhart于1995年提出,目前已被广泛应用于各个领域。
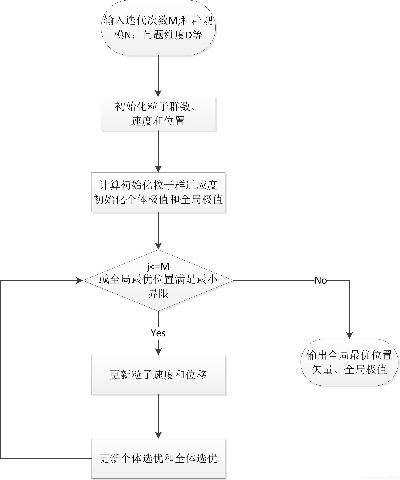
PSO算法的基本原理是通过不断地迭代来更新每个粒子的速度和位置,使得整个群体的适应度函数不断地向最优解靠近。每个粒子在搜索空间中随机生成一个初始位置和速度,并根据自己的适应度函数和群体的最优适应度函数来更新自己的速度和位置。其中,每个粒子的速度和位置更新公式如下:
v[i][j] = w*v[i][j] + c1*r1*(pbest[i][j] - x[i][j]) + c2*r2*(gbest[j] - x[i][j])
x[i][j] = x[i][j] + v[i][j]
其中,v[i][j]表示第i个粒子在第j个维度上的速度,x[i][j]表示第i个粒子在第j个维度上的位置,w为惯性因子,c1和c2分别为自我认知因子和社会认知因子,r1和r2为0到1之间的随机数,pbest[i][j]为第i个粒子在第j个维度上的最优位置,gbest[j]为整个群体在第j个维度上的最优位置。
PSO算法的优点是易于实现,不需要对目标函数进行求导,具有全局优化能力,可以处理非线性、非凸、高维、多峰等复杂问题。缺点是容易陷入局部最优解,收敛速度较慢,对参数的选择较为敏感。
PSO算法已经被广泛应用于优化问题,如机器学习、数据挖掘、智能控制、图像处理、信号处理等领域。在机器学习中,PSO算法可以用于神经网络的训练、特征选择、模型优化等方面;在数据挖掘中,PSO算法可以用于聚类分析、关联规则挖掘、异常检测等方面;在智能控制中,PSO算法可以用于PID控制、模糊控制、自适应控制等方面;在图像处理和信号处理中,PSO算法可以用于图像分割、滤波、压缩、特征提取等方面。
总之,粒子群智能算法是一种十分重要的优化算法,具有广泛的应用前景。







