高斯函数概述
高斯函数又称正态分布函数，是数学中常见的一种连续概率分布函数。高斯函数可以用来描述自然界中很多现象的分布规律，例如人的身高、体重等。
高斯函数在机器学习中的应用
1. 高斯混合模型
高斯混合模型是一种常用的聚类算法，它假设数据集中的样本是由多个高斯分布组成的混合体。通过对样本的聚类，可以更好地理解数据集的分布规律。
2. 高斯朴素贝叶斯分类器
高斯朴素贝叶斯分类器是一种常用的分类算法，它假设特征的分布符合高斯分布。通过对样本的特征值进行高斯分布拟合，可以计算出样本属于某个类别的概率。
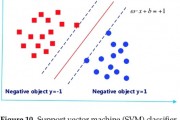
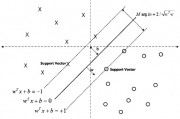
3. 高斯核函数
高斯核函数是支持向量机（SVM）中常用的核函数之一，它可以将非线性可分的数据映射到高维空间中进行分类。高斯核函数的本质是对数据进行高斯分布拟合，从而实现对非线性数据的分类。
4. 高斯过程回归
高斯过程回归是一种非参数回归算法，它通过对数据进行高斯分布拟合，得到一个高斯过程模型。高斯过程模型可以对数据进行预测，并给出一个置信区间，从而更好地理解数据的分布规律。
高斯函数在机器学习中有着广泛的应用，它可以用来描述数据的分布规律，从而实现聚类、分类、回归等任务。在实际应用中，我们需要根据数据的特点选择合适的高斯函数应用于机器学习任务中。
版权声明：
内容均收集于互联网,有侵权或不妥之处,请联系我们删除。敬请谅解！
