本文主要涉及的问题或话题是。傅立叶变换是一种基础的数学工具，可以将信号从时域转换为频域，广泛应用于信号处理、图像处理、声音处理等领域。在人工智能中，傅立叶变换也有着重要的应用。
Q1. 什么是傅立叶变换？
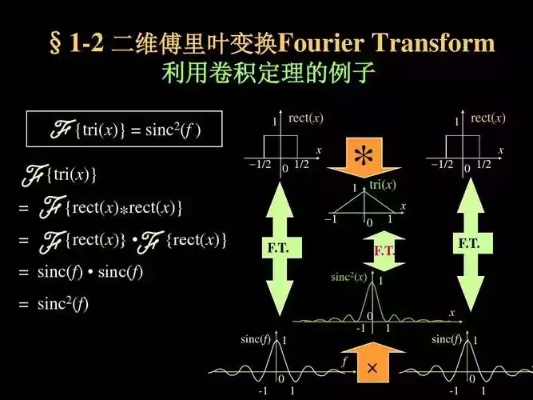
A1. 傅立叶变换是一种数学工具，可以将信号从时域转换为频域。它将一个复杂的信号分解成若干个简单的正弦波或余弦波的叠加，每个正弦波或余弦波都有不同的频率、幅值和相位。傅立叶变换可以应用于信号处理、图像处理、声音处理等领域。
Q2. 傅立叶变换在人工智能中有哪些应用？
A2. 傅立叶变换在人工智能中有多种应用。其中比较典型的应用包括：
1. 图像处理：傅立叶变换可以将图像从时域转换为频域，从而实现图像的滤波、可以使用傅立叶变换将图像分解成若干个频率分量，然后去除高频噪声，最后再将图像转换回时域。
2. 语音识别：傅立叶变换可以将语音信号从时域转换为频域，从而实现语音信号的特征提取。可以使用傅立叶变换将语音信号分解成若干个频率分量，然后提取出每个频率分量的幅值和相位，作为语音信号的特征。
3. 信号处理：傅立叶变换可以将信号从时域转换为频域，从而实现信号的滤波、可以使用傅立叶变换将信号分解成若干个频率分量，然后去除高频噪声，最后再将信号转换回时域。
Q3. 有哪些优势？
A3. 有以下优势：
1. 可以将信号从时域转换为频域，从而实现信号的滤波、
2. 可以将信号分解成若干个频率分量，从而实现信号的特征提取。
3. 可以提高信号处理的速度和效率，从而实现实时处理。
4. 可以应用于多种信号处理领域，具有广泛的适用性。
总之，傅立叶变换在人工智能中有着重要的应用，可以提高信号处理的速度和效率，从而实现实时处理，具有广泛的适用性。
版权声明：
内容均收集于互联网,有侵权或不妥之处,请联系我们删除。敬请谅解！
