粒子群算法是一种基于群体行为的智能算法，它是通过对群体中每个个体的位置和速度进行调整，从而实现对整个群体的优化。本文将探究粒子群算法在智能优化中的应用。
粒子群算法原理
粒子群算法的基本原理是通过模拟鸟群或鱼群等群体行为，来实现对整个群体的优化。在算法中，每个个体被称为粒子，每个粒子都有自己的位置和速度，位置表示个体的解，速度表示个体在解空间中的搜索方向。每个粒子都有自己的适应度函数，用于评价个体的解的好坏。在算法中，每个粒子都会根据自己当前的位置和速度，以及群体中最优解的位置，来更新自己的速度和位置，从而实现对整个群体的优化。
粒子群算法流程
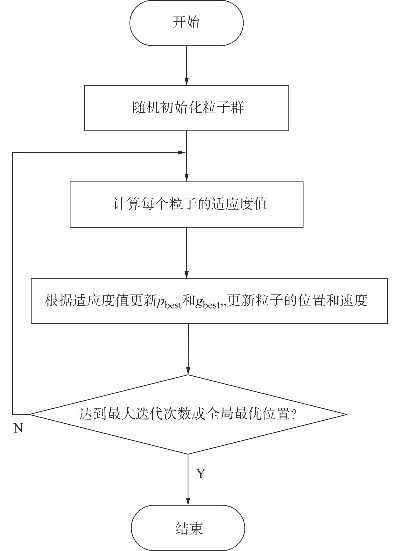
1. 初始化粒子群的位置和速度；
2. 计算每个粒子的适应度函数；
3. 更新全局最优解和每个粒子的最优解；
4. 更新每个粒子的速度和位置；
5. 重复步骤2-4，直到满足终止条件。
粒子群算法优点
1. 算法简单易实现；
2. 收敛速度快；
3. 适用于多维、非线性、多峰等复杂问题。
粒子群算法应用
1. 优化问题：粒子群算法可以应用于各种优化问题，如函数优化、组合优化、约束优化等；
2. 特征选择：粒子群算法可以用于特征选择问题，通过对特征子集进行搜索，找到最优的特征子集；
3. 神经网络训练：粒子群算法可以用于神经网络的训练，通过对神经网络的权值和偏置进行搜索，找到最优的网络参数。
粒子群算法的改进
1. 改进粒子的初始化方法；
2. 改进粒子的速度更新方法；
3. 引入惯性权重，平衡全局搜索和局部搜索；
4. 引入自适应权重，自动调整惯性权重。
粒子群算法是一种基于群体行为的智能算法，它可以应用于各种优化问题，特征选择和神经网络训练等领域。在使用粒子群算法时，需要根据具体问题调整算法的参数，以达到最优的效果。
版权声明：
内容均收集于互联网,有侵权或不妥之处,请联系我们删除。敬请谅解！
