人工智能算法数学:探索人工智能算法与数学的关系
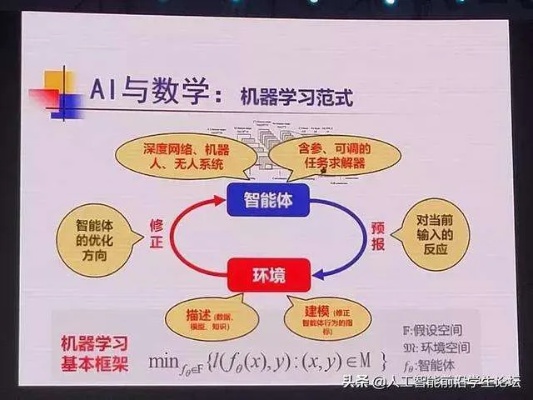
人工智能(AI)是一种在计算机系统中模拟人类智能的技术,它已经在各种领域得到广泛应用。其中,算法是实现人工智能的核心组成部分,数学则是支撑算法的基础。本文将探索人工智能算法与数学的关系,并介绍一些与该领域相关的数学概念。
一、人工智能算法与数学
人工智能算法是一种通过计算机程序实现智能行为的方法。它们可以通过模拟人类思维和行为来解决各种问题,例如图像识别、语音识别和自然语言处理等。这些算法的实现需要使用数学方法,例如线性代数、微积分、概率论和统计学等。
例如,神经网络是一种广泛使用的人工智能算法,它通过模拟人脑的神经元来实现智能行为。神经网络中的每个神经元都有一个与之相关的权重,这些权重可以通过数学方法进行优化,以使神经网络的输出与期望输出之间的误差最小化。这种优化方法称为反向传播算法,它是基于微积分和梯度下降的数学理论实现的。
另一个例子是遗传算法,它是通过模拟自然选择来优化问题解决方案的一种算法。在遗传算法中,问题解决方案被表示为一组“基因”,这些基因可以通过交叉和变异等操作进行修改,以产生更好的解决方案。这些操作的实现同样需要使用数学方法,例如概率论和统计学。
二、与人工智能算法相关的数学概念
除了上述数学方法之外,还有一些与人工智能算法相关的数学概念。以下是其中一些概念的简要介绍:
1. 线性代数
线性代数是一种研究向量、矩阵和线性方程组等数学对象的学科。它在人工智能算法中得到了广泛应用,例如神经网络中的权重和偏置可以表示为矩阵和向量形式。线性代数还可以用于解决图像和语音等数据类型的问题。
2. 概率论和统计学
概率论和统计学是研究随机现象的学科。在人工智能算法中,这些方法可以用于处理不确定性问题,例如分类和聚类等问题。它们还可以用于评估算法性能和进行模型选择等任务。
3. 最优化
最优化是研究如何在一定约束条件下寻找最优解的学科。在人工智能算法中,最优化方法可以用于优化神经网络的权重和偏置、遗传算法的基因等。
三、结论
人工智能算法是一种基于数学方法实现智能行为的技术。数学在人工智能算法中扮演着重要的角色,例如线性代数、微积分、概率论和统计学等。最优化方法也是人工智能算法中常用的数学工具之一。了解这些数学概念可以帮助我们更好地理解人工智能算法的原理和应用。






